Searching and Big O Notations
Contents
Searching and Big O Notations#
In the last chapter, we discussed that several versions of the code might exist to achieve a task. However, some or just one version of the code may be efficient. Therefore, one of the units to measure the efficiency of a code is to calculate the number of steps required to achieve a desired result. We further explored that in a given data structure, the efficiency of a data structure varies with different operations, such as reading, searching, insertion, and deletion. In this chapter, we dive a little deeper and discuss what other factors can affect the performance of a code.
Organization of data#
Let’s extend our discussion about an array data structure. Assume that an array is filled with an integer data type with random elements with no repetition of elements. Let’s choose a real-world example - an array data structure filled with the last four digits of an SSN. For simplicity reasons, assume that the array data structure is the best choice for storing the number. The figure shows the array with elements stored randomly. The user searches for a particular SSN in an array. The processor starts the search from index 0 and then continues to search until the desired element is found. If the data is the last element (worst-case scenario), the search traverses the entire array’s length. Hence, the number of steps in searching a data element of a worst-case scenario would be N, where N is the length of an array. On the contrary, inserting data into an array would require just one step. The new data appends at the end of the array and do not require any element shifting, see Fig. 3
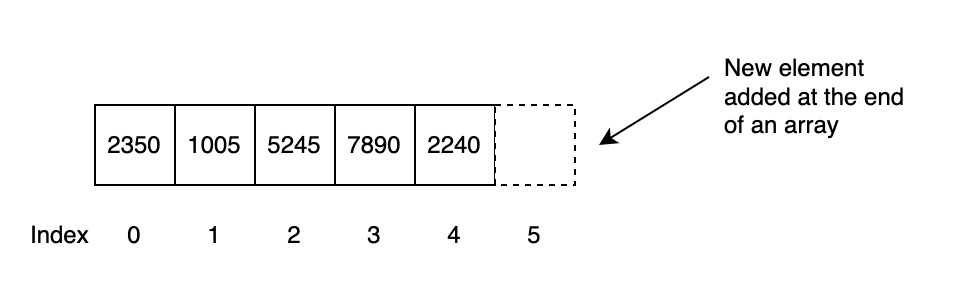
Fig. 3 Insertion on a unsorted array#
Let’s extend the above assumption, but this time, the elements in the array are sorted. So, for example, if value 5245 is searched in an array, the search stops where the value is just greater than 5245; in this example, the search stops at index 4. This search is called a linear search.
The following is the pseudocode of the basic linear search algorithm.
Given a list \(L\) of \(n\) elements with values or records \(L_0\) …. \(L_{n−1}\), and target value \(T\), the following subroutine uses linear search to find the index of the target \(T\) in \(L\).
1. Set i to 0.
2. If Li = T, the search terminates successfully; return i.
3. Increase i by 1.
4. If i < n, go to step 2. Otherwise, the search terminates unsuccessfully.
Does linear search perform better when arrays are sorted over unsorted?
Unfortunately, the answer is no; under the worst-case scenario, the linear search would use the ‘N’ number of steps where ‘N’ is the number of elements in an array regardless of whether arrays are sorted or not sorted.
Furthermore, keeping the array in a sorted state before applying any search operation does require some processing. For example, inserting an integer value in an array does require comparison and shifting elements so that the new value goes into the correct place. The new number is compared with the each element in an array until the correct location is found, see Fig. 4
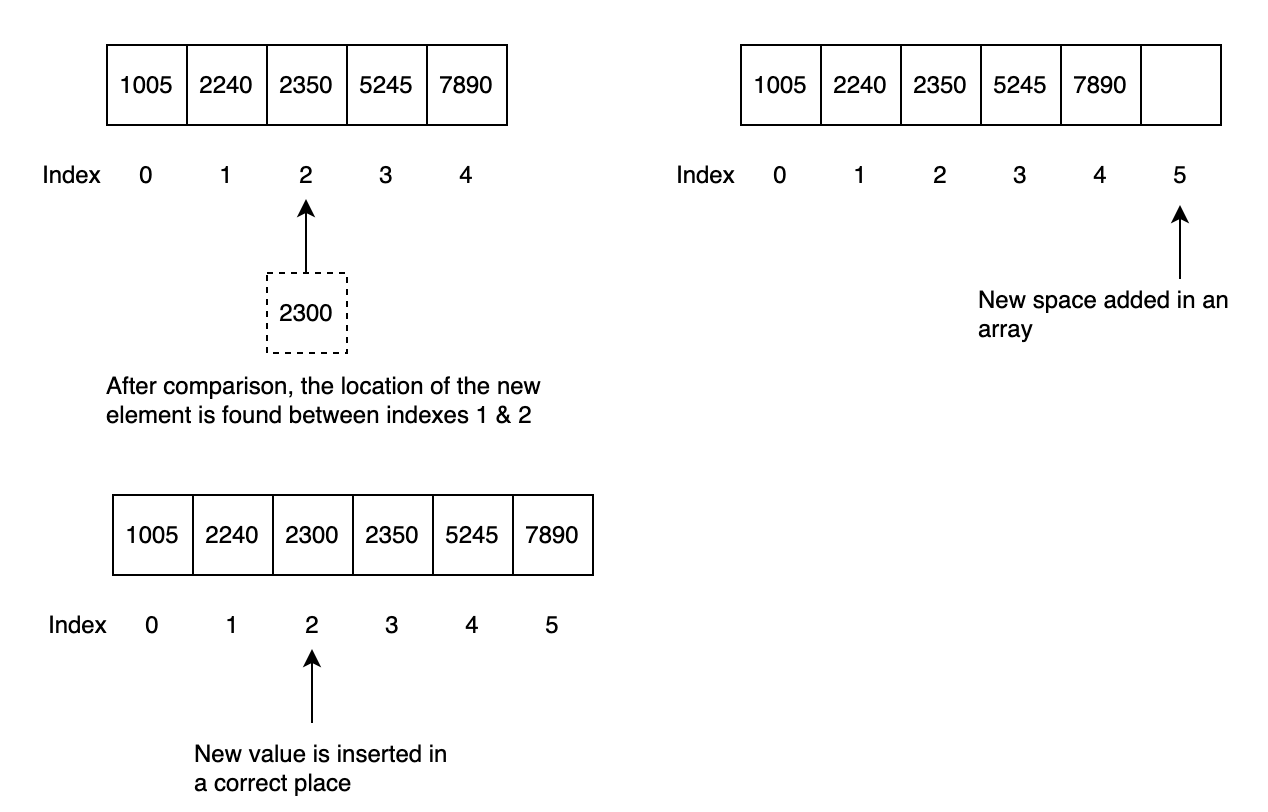
Fig. 4 Insertion on a sorted array#
Based on the above discussion, linear search on sorted arrays does not improve performance. Furthermore, there is an overhead of sorting arrays, so why do we even bother sorting an array?
Indeed, the linear search algorithm is inefficient regardless of whether arrays are sorted or not. However, sorted arrays unlock other search algorithms, such as binary search, which works at a blazing-fast speed compared to linear search algorithms.
Binary search#
Binary search works on sorted arrays. Binary search begins by comparing an element in the middle of the array with the target value. If the target value matches the element, its position in the array is returned. If the target value is less than the element, the search continues in the lower half of the array. If the target value is greater than the element, the search continues in the upper half of the array. By doing this, the algorithm eliminates the half where the target value cannot lie in each iteration.
See the animation1 of binary search algorithm.
Procedure#
Given an array \(A\) of \(n\) elements with values or records \(A_0\),\(A_1\),\(A_2\),…,\(A_{n-1}\) sorted such that \(A_0\) \(\leq\) \(A_1\) \(\leq\) \(A_2\) \(\leq\) … \(\leq\) \(A_{n-1}\), and target value \(T\), the following subroutine uses binary search to find the index of \(T\) in \(A\).[Knu98]
Set \(L\) to 0 and \(R\) to \(n-1\).
If \(L\) \(\gt\) \(R\), the search terminates as unsuccessful.
Set \(m\) (the position of the middle element) to the floor of \(L+R\over2\), which is the greatest integer less than or equal to \(L+R\over2\).
If \(A_m\) \(\lt\) \(T\), set \(L\) to \(m+1\) and go to step 2.
If \(A_m\) \(\gt\) \(T\), set \(R\) to \(m-1\) and go to step 2.
Now \(A_m\) = \(T\), the search is done; return \(m\).
In mathematics and computer science, the floor function is the function that takes as input a real number \(x\), and gives as output the greatest integer less than or equal to \(x\), denoted \(\lfloor x\) \(\rfloor\) or floor\((x)\). For example, the floor value of 3.7 is 3, because the number of integers less than 3.7, is 3, 2, 1, 0 and so on. So, the highest integer will be 3.
Pseudocode#
function binary_search(A, n, T) is
L := 0
R := n − 1
while L ≤ R do
m := floor((L + R) / 2)
if A[m] < T then
L := m + 1
else if A[m] > T then
R := m − 1
else:
return m
return unsuccessful
Comparison of Linear and Binary search#
The binary search does not provide a significant advantage over a linear search algorithm. In a linear search algorithm, if we are searching for a value that exists in the last cell of an array, then the search algorithm would iterate all the elements in an array. This case is an example of a worst-case scenario. The linear search takes N number of steps where N is the number of elements in an array. On the contrary, the binary search would take \(log_2N\) steps. The result of \(log_2N\) will be rounded up to the nearest decimal value. For example, if there are 100 elements in an array, the linear search would take 100 steps, whereas the binary search would finish the search in just 7 steps. The Fig. 5 shows that under the worst-case scenario, the number of steps in the binary search increases by one each time when the number of elements doubles.
\(log_2N\) is calculated as \(log_{10} N \over log_{10}2\), where \(N\) is the number of elements in an array. If there are 1000 elements, the binary search would take 10 steps to perform the search. Remember the result is rounded up to the nearest decimal integer.
Remember that sorted arrays are only efficient in some scenarios. As we discussed, insertion in sorted arrays is slower than in unsorted arrays. However, there is a tradeoff in speed; slower insertion but fast search. If an application performs many insertions but less searching, then unsorted arrays would be a better choice. It is up to the programmer to analyze and select the correct data structure.
Fig. 5 Linear and binary search comparison#
Big O Notations#
As discussed previously, each algorithm’s efficiency is primarily based on the number of steps it takes. The number of steps an algorithm takes is based on the worst-case and best-case scenarios, and the number of elements in an array, and so on.
To help ease communication regarding time complexity, computer scientists have borrowed a concept from the world of mathematics to describe a concise and consistent language around the efficiency of data structures and algorithms, as known as Big O Notation.
In other words, big O notation is used to compare efficiencies between algorithms to achieve a task. It’s the letter O not the number 0. So what does the O stand for? ‘Order’, or ‘order of complexity’. For example, as discussed before that the linear search takes N steps. Therefore, in the language of big O notation, the linear search algorithm is expressed as O(N). The efficiency of each algorithm is dependent upon a scenario. I defined scenarios as worst-case, average-case, and best-case scenarios. For example, under a linear search algorithm, if the search element is the first element in the array, the complexity will be O(1). On the contrary, the complexity will be O(N) if the search element is the last element in the array. Generally speaking, the algorithm’s efficiency is gauged under the worst-case scenario.
The above is more of a conservative approach. However, if you know how inefficient an algorithm can get in a worst-case scenario, the better we are prepared for the worst and may strongly impact our choices.
O(1) algorithm complexity is independent of the number of elements in an array. For example, the complexity of inserting an element in an unsorted array is O(1) because it will take only a step to insert the element without shifting an element.
Big O tells you how the number of steps increases as the data changes.
Fig. 6 is a comparison between time complexity of \(O(n)\), \(O(log_2n)\) and \(O(1)\). The comparison suggests that an algorithm with a time complexity of \(O(log_2n)\) always performs better than \(O(n)\). Furthermore, the complexity of \(O(1)\) will always perform better regardless of n.
Fig. 6 Big O comparisons between O(n), O(log n), and O(1)#
\(O(1)\) example#
""" Code written in Python """
data = ["apples","oranges","grapes","pineapple"]
data.append("kiwi")
print(data[0])
In the above example, a new element is appended at the end of the list. The insertion of a new element does not require any shifting of elements. Furthermore, the data is printed at index 0.
\(O(n)\) example#
""" Code written in Python """
data = ["apples","oranges","grapes","pineapple"]
for i in data:print(i)
In the above example, a list is defined, and the for loop iterates over the list and prints the element in each iteration. Hence, the for loop will run equal to the length of the list. This is an example of \(O(n)\) complexity.
\(O(log_2n)\) example#
Conclusion#
There is no single algorithm that is perfect for every situation. For example, sorted arrays provide improvements in terms of searching an element using a binary search; however, at the cost of increasing complexity when inserting elements in the sorted array. On the contrary, if adding data is the main task, standard arrays may be a better choice due to the faster insertion rate. The Big-O notation is used to find the worst-case scenario of the time it takes an algorithm to do its job.
