Why learn data structures?#

The Data Structures course is one of the most important, and I think every student pursuing a software engineering degree takes this course at the undergraduate level. The data structure course is all about creating efficiencies in the code. A programmer can write an application and get the desired result. However, the question is, “Does the code written with efficiency in mind”.

Efficiency can be defined as how the code utilizes space and time.

For example, look at these two functions, which print all the even numbers; however, one code runs faster than the other.

""" The following code is written in Python """
""" Version 1 """
def print_numbers_version_one():
    number = 2
    temp = 1
    while number <= 100:
        temp += 1
        # if number is even, print it:
        if number % 2 == 0:
            print(number)
        number += 1
    print("Loop executed",temp,"times")

""" Version 2 """
def print_numbers_version_two():
    number = 2
    temp = 0
    while number <= 100:
        temp += 1
        print(number)
    # increase number by 2, which, by definition, is the next even number:
        number += 2
    print("Loop executed",temp,"times")

Which of these functions do you think runs faster? If you said Version 2, you’re right. This is because Version 1 loops 100 times, while Version 2 only loops 50 times. The first version then takes twice as many steps as the second version.

We are living in the data age. Big data—information of extreme volume, diversity, and complexity is everywhere. Enterprises, organizations, and institutions are beginning to recognize that this massive volume of data can potentially deliver high value to their business. The explosion of data has led to significant innovations in various technologies, all revolving around how this massive volume of data can be efficiently captured, stored, and processed to extract meaningful insights that will help them make better decisions much faster, perform predictions of various outcomes, and so on.

A data structure is a way of organizing, storing, and performing operations on data. Operations performed on a data structure include accessing or updating stored data, searching for specific data, inserting new data, and removing data. Basic and advanced data structures are used in almost every program or software system that has been developed. Table 1 provides a list of basic data structures and a brief description. This is not a complete list of data structures. Instead, I will re-visit the following data structures in detail.

Table 1 Brief description of data structures#
Data Structure	Description
Record	A record is the data structure that stores subitems, often called fields,with a name associated with each subitem.
Array	An array is a data structure that stores an ordered list of items, where each item is directly accessible by a positional index.
Linked list	A linked list is a data structure that stores an ordered list of items in nodes, where each node stores data and has a pointer to the next node.
Binary tree	A binary tree is a data structure in which each node stores data and has up to two children, known as a left child and a right child.
Hash table	A hash table is a data structure that stores unordered items by mapping (or hashing) each item to a location in an array.
Heap	A max-heap is a tree that maintains the simple property that a node’s key is greater than or equal to the node’s childrens’ keys. A min-heap is a tree that maintains the simple property that a node’s key is less than or equal to the node’s childrens’ keys.
Graph	A graph is a data structure for representing connections among items, and consists of vertices connected by edges. A vertex represents an item in a graph. An edge represents a connection between two vertices in a graph.

Choosing data structures#

The selection of data structures used in a program depends on the type of data being stored and the operations the program may need to perform. Choosing the best data structure often requires determining a good balance given expected uses.

It is essential to select the data structure which performs well for a given task. For example, if a program requires fast insertion of a new patient in a hospital database, a linked list data structure is a better choice over arrays, see Fig. 1.

_images/linked-list.png — Fig. 1 Linked-list and arrays#

What are algorithms?#

An algorithm is simply a set of instructions for completing a specific task.

The process of preparing food is technically an algorithm. The pasta-preparation algorithm to cook food requires the following steps:

Boil water in a pan
Add salt and oil
Add pasta to a boiling water
Check if the pasta is cooked
Drain water if pasta is cooked

When applied to computing, an algorithm describes a sequence of steps to achieve a particular task. When we write any code, we create algorithms for the processor to follow and execute.

The first step in achieving a particular task is to write a pseudocode which involves writing steps in plain human language. Pseudocode often uses structural conventions of a standard programming language but is intended for human reading rather than machine reading. Out of many articles, there is a very well-written article that explains why we use pseudocode at all.1

Practical applications#

Computational problems can be found in numerous domains, including e-commerce, internet technologies, biology, manufacturing, transportation, etc. Algorithms have been developed for numerous computational problems within these domains.

A computational problem can be solved in many ways, but finding the best algorithm to solve a problem can be challenging. However, many computational problems have common subproblems for which efficient algorithms have been developed. Table 2 describe a computational problem within a specific domain and list a common algorithm that can be used to solve the problem.

Table 2 Example computational problems and common algorithms#
Application domain	Computational problem	Common algorithm
DNA analysis	Given two DNA sequences from different individuals, what is the longest shared sequence of nucleotides?	Longest common substring problem: A longest common substring algorithm determines the longest common substring that exists in two input strings.
Search engines	Given a product ID and a sorted array of all in-stock products, is the product in stock and what is the product’s price?	Binary search: The binary search algorithm is an efficient algorithm for searching a list. The list’s elements must be sorted and directly accessible (such as an array).
Navigation	Given a user’s current location and desired location, what is the fastest route to walk to the destination?	Dijkstra’s shortest path: an algorithm for finding the shortest paths between nodes in a graph.

Basic data structure: Arrays#

As you have already known that arrays are the most basic data structures. An array is a data structure that stores data of the same type sequentially in memory. In literature, many authors use the term “arrays is a kind of a list which stores data of the same type”. However, I would avoid using the word “list” because the list is another kind of data structure, and there is a possibility that a reader might get confused between an array and a list.

The computer memory can be viewed as a giant collection of cells, see Fig. 2. Each cell has an address, and the data is stored under each address. When a programmer defines an array, a compiler or an interpreter search for a contiguous space. In Fig. 2, the user creates an array of size 4. Each element in an array is indexed and can be referenced by using an index.

For example, an array can be defined as:

user_array = ["red","blue","green","yellow"]

The user_array has a base address of 100 and the first, second, third, and fourth elements can be accessed by base address + index. For example, the elements can be accessed like user_array[0] for the first element, and so on.

The size of an array is equal to how many data elements the array holds. The index of an array is always an integer number that identifies where a piece of data lives inside the array. The starting index integer is based on the programming language. For example, Java, Python, C, and C++ languages use index 0, however, Fortran, R, Julia, and Matlab use index 1. This is not a complete list of all the languages.

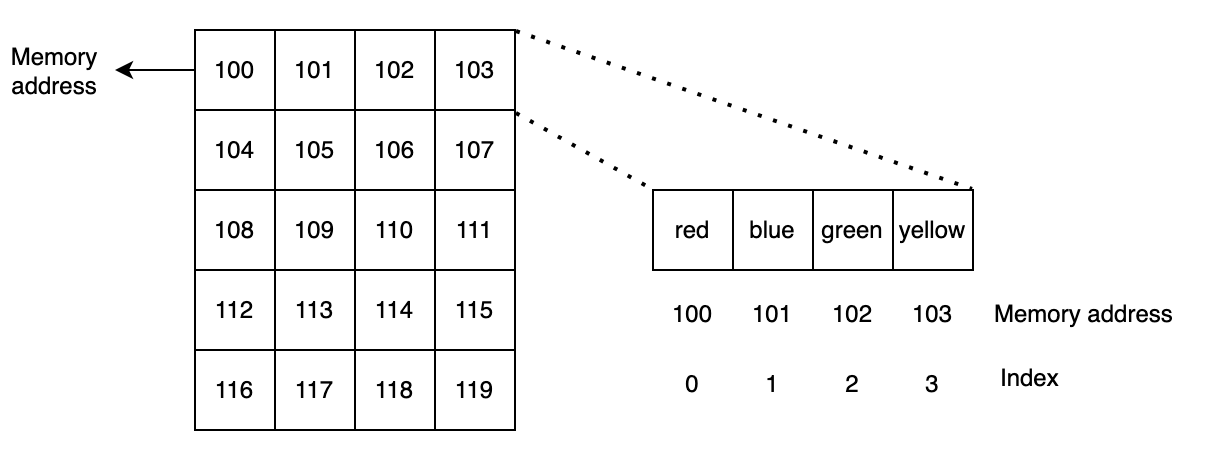
_images/memory_mapping.png — Fig. 2 Array to memory mapping#

Operations on Arrays#

The following are the most basic operations which apply to many data structures.

Read: Reading refers to looking up the data at a certain index. For example, read data at index 1. In a programming language, this can be written as user_array[1]. This operation would take a single step to retrieve an element.

Insert: Insertion refers to adding an element to an existing array which means increasing the size of an array. The insert operation on an array can be done at any index location. The insert operation can take one or more steps depending on the location of the inserted element.

Delete: Deletion refers to removing an existing value from an array. After removal, the array rearranges the size and the index numbers. The delete operation on an array can be done at any index location. The delete operation can take one or more steps depending on the location of the deleted element.

Search: Search refers to looking for a particular element in an array. The search operation can take one or more steps depending on the location of the searched element.

The need for measuring speed#

Anyone with a little programming experience can write code and solve a problem. However, does the code written most efficiently? As I have already pointed out earlier that, version 2 performs better because it takes half the steps as compared to version 1.

For programmers, it is very important to know the speed of an operation on any data structure. You may think that the unit to measure speed is time (seconds). The time may not be an accurate unit to measure the data structure operation’s speed because each processor’s clock speed is different, and processors have the ability to execute multiple instructions/clock cycle. Hence, there will be variations in time among different processors.

There is a misconception about comparing a processor’s speed in the context of the clock cycle. Comparing processor speeds of different generations or brands does not reflect the true comparisons. For example, which processor outperforms well; (an old generation processor at 4 GHz or a new generation processor at 3 GHz)? Seems like 4 GHz will outperform well than 3 GHz; however, this is not always the case. Such comparison is like comparing Apples to Oranges. A CPU with a higher clock speed of an old generation might be outperformed by a new generation CPU with a lower clock speed, as the newer architecture deals with instructions more efficiently. However, within the same generation of CPUs and the same brand, a processor with a higher clock speed will generally outperform a processor with a lower clock speed across many applications. I found a few articles on the Internet that talks about processor clock speed and Intel processor naming conventions which I think are very useful to know.2 3

The most accurate unit to measure the efficiency of a code is steps.

Number of steps in read operation Since arrays are all indexed and if the base address of an array is known, then simply adding the index number to the base address will reveal the data. For example:

user_array = ["red","blue","green","yellow"]
print("user_array[0]")

The above code gets the element at index 0 in one step. The base address of user_array is 100, see Fig. 2.

In data structures, an operation that takes just a single step is considered the fastest type of operation. In a nutshell, if you have lots of data, selecting an array data structure for reading is a smart choice. Regardless of the number of elements in an array N, the read operation will always be 1.

Number of steps in insert operation The number of steps required to perform an insert operation on an array is dependent on where the insertion takes place on an array.

For example, if the insertion takes place at the end of the array, then the compiler/interpreter would increase the size of an array and allocate a memory address. The step needed to add an element at the end of an array is 1. However, inserting an element at the start of an array (at index 0) would require shifting all the elements and then insert an element at index 0. If the array size is 100, it would take 100 steps to shift and 1 step to insert an element, or better say N+1 steps; where N is the number of elements. The constant 1 is the step to add an element.

Number of steps in search operation The number of steps required to perform a search operation on an array is dependent on where is the element in an array.

For example, if the element is at index 0, then it would take only a single step. If the element is at the last index, then it would take N steps.

Number of steps in delete operation Deletion from an array is the process of eliminating the value at a particular index. The number of steps required to perform a delete operation on an array is dependent on where the deletion takes place on an array. If the deletion happens at the last index, there is no need to shift elements in an array. It would take just one step to perform the deletion.

However, if the deletion happens at index 0, then one step for deletion and N-1 steps to shift the elements in an array. For example, if an array size is 100, one step for deletion and 99 steps to shift elements in an array, which gives a total of N steps.

The following Table 3 summarizes the number of steps of best and worst-case scenarios on various operations on an array. N is the number of elements in an array.

Table 3 Time complexity of array data structure#
Operations	Best case	Worst case
Read	1	1
Insert	1	N+1
Search	1	N
Delete	1	N

Conclusion#

Choosing the proper data structure for your application is crucial, mainly when the software deals with a large amount of data and continuously performs read, insert, search and delete operations. It is a programmer’s job to analyze the time complexity of a data structure to better prepare the software when the demand is high. In this chapter, you have learned what an algorithm is, why you need an algorithm, and how to think of a data structure from the time complexity point of view.

1: https://www.cs.cornell.edu/courses/cs482/2003su/handouts/pseudocode.pdf
2: https://www.intel.com/content/www/us/en/gaming/resources/cpu-clock-speed.html
3: https://www.intel.com/content/www/us/en/gaming/resources/gaming-processor-names.html

Data Structures in C++

Why learn data structures?

Contents